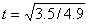FISIKA COOL & IS THE BEST

1. sebuah benda berputar pada suatu sumbu dengan perpindahan sudut yang besarnya dinyatakan dalam persamaan θ = 8t2 – 5t + 3 (θ dalam radian dan t dalam sekon). Tentukan:
1. berapa besar perpinahan sudut pada t = 0 dan t = 3 sekon
2. berapa besar kecepatan sudut pada t = 0 dan t = 3 sekon
3. berapa laju liner sebuah titik yang berjarak 20 cm dari sumbu putaran pada saat 2 sekon
4. berapa percepatan sudut benda

Dik : θ = 8t2 – 5t + 3

Dit :

a. θ <-- pada saat t = 0 dan t = 3 sekon

b. ω<-- pada saat t = 0 dan t = 3 sekon

c. V <-- r = 20 cm = 0,2 m dan t = 2 sekon

d. Ά

Jawab

a. θ = 8t2 – 5t + 3

t = 0 <-- θ = 8t2 – 5t + 3

θ = 8(0)2 – 5(0) + 3

θ = 3 rad

t = 3<-- θ = 8t2 – 5t + 3

θ = 8(3)2 – 5(3) + 3

θ = 72 – 15 + 3

θ = 60 rad

b. ω = d θ / dt

ω = d(8t2 – 5t + 3)/dt

ω = 16t – 5

t = 0 <--ω = 16t – 5

ω = 16(0)– 5

ω = 5 rad/sekon

t = 3 <-- ω = 16t – 5

ω = 16(3) – 5

ω = 43 rad/sekon

c. ω = 16t – 5

ω = 16t – 5

t = 2 ß ω = 16t – 5

ω = 16(2) – 5

ω = 27 rad / sekon

V = ω . r

V = 27 X 0.2

V = 5.4 m/s

d. Percepatan sudut (ά)

ά = d(16t – 5)/dt

ά = 16 rad/s2

2. Sebuah titik materi di tepi roda berjari- jari 1 meter. Mula- mula berputar dengan laju 2 rad/s lalu dipercepat dengan percepatan 3 rad/s2. Tentukan

a. Persamaan posisi suduut titik materi

b. Kecepatan liner titik materi pada saat t = 2 sekon

Dik :

r = 1 m

ω = 2 rad / sekon

ά = 3 rad / sekon

Dit :

1. Persamaan posisi sudut titik materi
2. V pada saat t = 2 sekon

Jawab

a. Persamaan posisi suduut titik materi

θ = θo + ∫ ω dt + ∫∫ ά dt . dt

θ = 0 + ∫ 2 dt + ∫∫ 3 dt . dt

θ = 2t + 3/2 t2

b. Kecepatan liner titik materi pada saat t = 2 sekon

V = r ω = r(ω + ∫ ω dt)

V = 1(2 + ∫ 3 dt)

V = 2 + 3t ß t =2 sekon

V = 2 + 3 (2)

V = 8 m/s

1. Suatu gelombang berjalan melalui titik P dan Q yang berjarak 8 cm dalam arah dari P dan Q. Pada saat t = 0 simpangan gelombang di A adalah 0. Jika panjang gelombang 12 cm dan amplitudonya = 4 cm maka tentukanlah simpanan di titik Q pada saat sutut fase titik P = 3 π / 2
Dit :
t= 0 <-- y = 0
A = 4 cm
X = 8 cm
λ = 12 cm

Dit: y saat θp = 3 π/2

Jawab
yQ = A sin 2 π(ft –x/ λ)
Δθ = 2 πΔφ
θQ – θP = 2π(Δx/ λ)
θQ – θP = 2 π(8 / 12)
θQ – 3/2 π = 4 / 3 π
θQ = 4 /3 π + 3 /2 π =(8 π +9 π) / 6
θQ = 17 π / 6
yQ = 4 sin θQ
= 4 sin (2π + 5 π/6)
= sin + 5 π/6
= 4 sin 150o
= 4 . ½
= 2 cm
2. Gelombang stasioner pada sebuah tali mempunyai persamaan simpangan y = 2 sin π cos 6 πx. (y, x1, dan t dalam SI)
a. amplitudo titik P yangterletak ada jarak 75 cm dari titik pantul
b. periode gelombang
Dk :
y = 2 sin π cos 6 πx
Dit : A & T
Jawab :
a. y = 2 sin π cos 6πx
= 2 cos 6πx sin 5πt
= A’ sin 5πt
A’= 2 cos 6πx
X = 0.75 m <-- A’ = 2 cos 6πx
= 2 cos 6π (0.75)
= 2 cos (2 . 2π + 0.5π)
= 2 cos 0.5π
b. y = 2 cos 6πx sin 5πt
Berdasarkan rumus : 2A cos 2π / λ * sin 2πt
Maka diperoleh :
5πt = 2πt / T
T = 2πt / 5πt
T = 2 / 5 sekon

1. Sebuh benda melakukan gerak harmmonik sederhana sepanjang Y. simpangannya berubah terhdap waktu sesuai dengan persamaan y = 4 sin (πt + π/t). Satuan y dalam meter dan t dalam sekon.
a. tentukan amplitude, frekuensi, dan periode gerak.
b. Hitung kecepatan dan percepatan benda pada waktu t
Dik:
y = A sin (ώt + π/t) meter
y = 4 sin (πt + π/t) meter
Dit :
a. Dari kedua persamaan diperoleh A = 4 meter dan ώ = π rad/s, sehingga 2πf = π atau f = 0.5 Hz dan
T = 1/f
= 1/ 0.5
= 2 sekon

b. Kecepatan merupakan turunan pertama dari persamaan simpangan , yaitu
V = dy/dt = d(4 sin (πt + π/4)) / dt
= 4π cos (πt + π/4) m/s

Percepatan merupakan turunan pertama dari persamaan kecepatan yaitu :
a = dv/dt = d(4π cos(πt + π/t)) / dt
= -4π2 sin(πt + π/t) m/s2

2. Massa sebuah benda yang bergerak secara harmonik adalah 400 kg pada frekuensi 25 Hz dan amplitude 5 cm. Hitunglah besar :
a. Percepatan maksimum getaran harmoniknya
b. Kecepatan harmonic getaran harmoniknya
c. Gaya maksimumnya.
Dik :
m = 400 kg
f = 25 Hz
A = 5 m
Dit :
a. a maksimum
b. V maksimum
c. F maksimum
Jawab
a. a maks = ώ2 A
= (2 πf)2 (5)
= (2π . 25)2.7,5
= 4π2.625.7,5 = 18.750π2 cm/s2
b. V maks= ώ A
= 2π f A
= 2π . 25 . 5 = 375π cm/s
c. F maks = ώ 2 m A
= (2πf)2 m A
= (2π . 25)2 . 400 . 5
= 5 . 106 π2 dyne

SOAL USAHA DAN ENERGI
1. Sebuah benda bemassa 0.25 kg brgerak dengan kecepatan 5 m/s dititik A pada lintasa gambar di samping. Berapa kecepatan benda dititik C? (g = 10 m/s2)
Dik:
m = 0.25 kg
vA = 5 m/s
g = 10 m/s2
hA = 1.5 m
hC = 2.5 m
Dit : Vc
Jawab
EMA = EMC
EKA + EPA = EKC + EPC
1/2 mv2A + mghA = 1/2mv2C + mghC
m(1/2v2A + ghA) = m(1/2v2C + ghC)
1/2v2A + ghA = 1/2v2C + ghC
½ (5 m/s2) + (10 m/s2) (1.5 m) = 1/2v2C + (10 m/s2) (2.5 m)
v2C = 5
vC = 2.24 m/s
2. Sebuah bola dilemparkan disebuah gedung yang tingginya 15 m. kecepatan awal bola ketika dilempar sama dengan 15 m/s dengan arah 30o diatas garis horizontal. Berapakah kelajuan bola sesaat sebelum menumbuk tanah? (g = 10 m/s2)
Dik
hA = 15 m
vA = 15 m/s
g = 10 m/s2
hB = 0
Dit : vB
Jawab
1/2V2A + mghA = 1/2V2A + mghB
1/2V2A + ghA = ½ V2B
½(15) + (10)(15) = 1/2V2B
VB = 22.91 m/s

1. Sebuah bola yang massanya 0.2 kg jatuh dari ketinggian 45 m. Waktu sentuh bola menumbuk tanah adalah 0.1 s sampai akhirnya bola berbalik dengan kecepatan 2 / 3 kali kecepatan ketika bola menumbuk tanah. Hitunglah

a. Perubahan momentum bola pada saat menumbuk tanah

b. Besar gaya yang bekerja pada bola akibat menumbuk tanah.

Dik

m = 0,2 kg

h = 45 m

Δt = 0,1 sekon

v’ = -2/3 v

v’ = -2/3 (30) = -20 m/s

a. Perubahan momentum

Δp = mΔv = m(v’ – v)

= (0,2) (-20 – 30)

= - 10 kg m/s

b. Gaya yang bekerja pada bola

FΔt = Δp

F = Δp / Δt = -10 / 0,1

F = - 100 N

2. Sebuah meteor yang bermassa 2000 kg yang bergerak menuju bumi menumbuk bumi dengan kecepatan 120 m/s. Jika massa bumi 6 x 10²⁴ kg, berapakah kecepatan bumi setelah tumbukan bila meteor akhirnya terbenam kebumi?

Dik :

m_m = 2000 kg

m_B = 6 x 10²⁴ kg

v _m = 120 m/s

v_B = 0

Tumbukan tidak elastis sama sekali

m_m v_m = (m_m + m_B) v’

v’ = (m_m v_m) / (m_m + m_B)

v’ = ((2000) (120)) / (2000 + 6 x 10²⁴)

v’ = 4 x 10^-24 m/s

1. Sebuah pesawat memerlukan 20 detik dan 400 m berjalan dilandasan pacu hingga mengangkasa dari keadaan diam. Kecepatan ketika meniggalkan lamdasan adalah.
Dik : S = 400 m
t = 20 detik
Dit: V
Jawab
S = Vot +1/2at2
400 = 0 + 1/2a.202
400 = ½ 400 a
400 = 200 a
a = 400/200
a = 2 m/s2

V = Vot + at
V = 0 + 2 . 20
V = 40 m/s
2. Sebuah bola di lemparkan keatas dengan kecepatan awal 30 m/s jjika percepatannya adalah 10 m/s2 kebawah. Berapa jarak titik tertinggi bola tersebut.
Dik: V = 30 m/s
a = 10 m/s2
Dit : S
Jawab
Vt = Vo + at
30 = 0 + 10 t
t = 30/10
t = 3 detik
S = Vot + ½ at2
= 30 + ½ 10 3
= 45 m
3. percepatan sebuah benda yang bergerak lurus sebagai fungsi dari waktu dinyatakan sebagai a = 12t – 30 (Satuan dalam SI) Jika kecepatan awal 5 m/s dan posisi awal 8 m dari titik asal tentukan kecepatan dan posisi sebagai fungsi dari waktu
Dik ; a = 12t – 30
Vo = 5 m/s
Xo = 8 m
Dit : V dan X (Fngsi dari waktu)
Jawab
V = ∫adt + Vo
= ∫(12t – 30)dt + 5
= 6t2 – 30t + 5

X = Xo + ∫V dt
= 8 + ∫(6t2 – 30t + 5)dt
= 8 + 2t3 – 15t2 + 5t
= 2t3 – 15t2 + 8